Specialty Finite Elements
Our coupled mixed-field mechanics models for piezocomposite laminates were extended to include non-linear effects arising due to large displacements & rotations. This has resulted in the development of a novel non-linear piezolaminate theory, a series of non linear finite-element formulations for active/sensory piezocomposite structures, and a new 8-node finite element, which all together have yielded unprecedented new analytical capabilities, some of them are enumerated below:
State-of-the-art computational methods
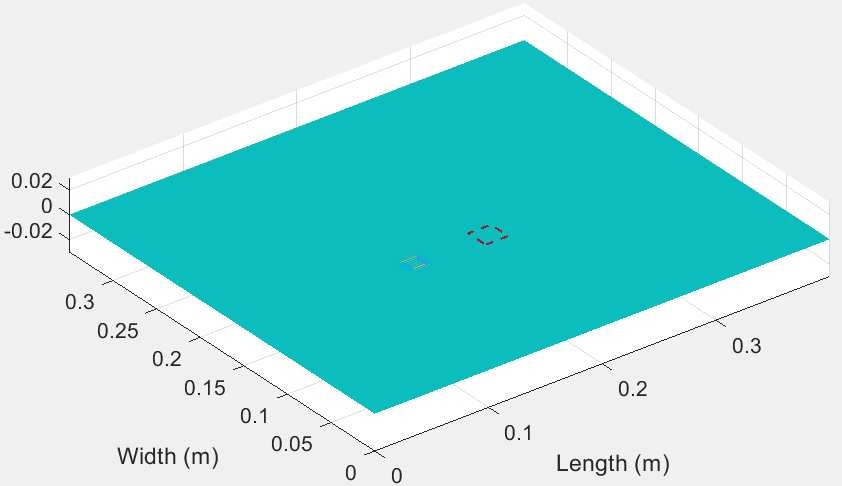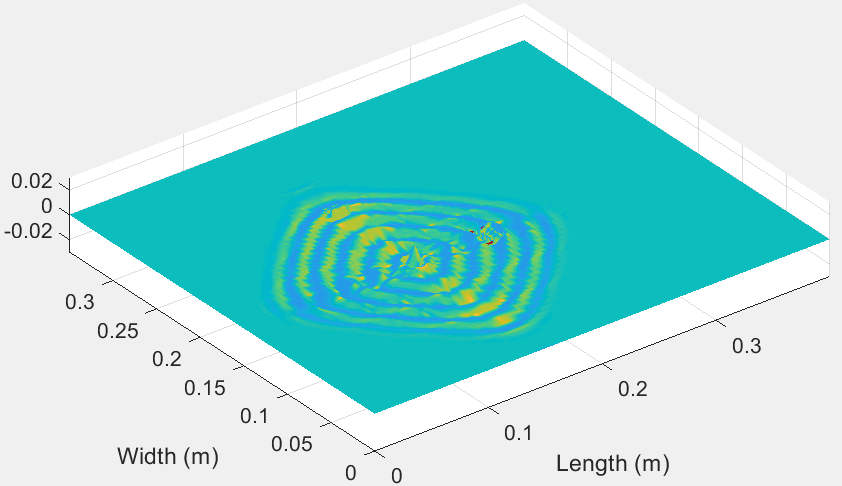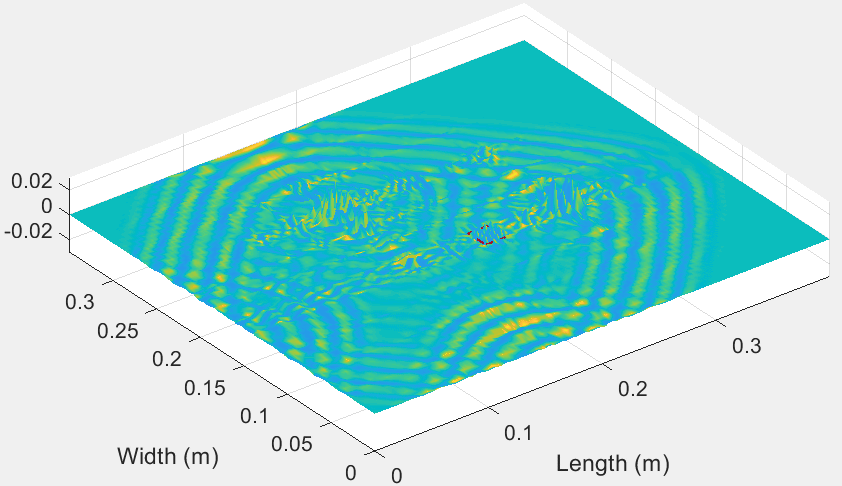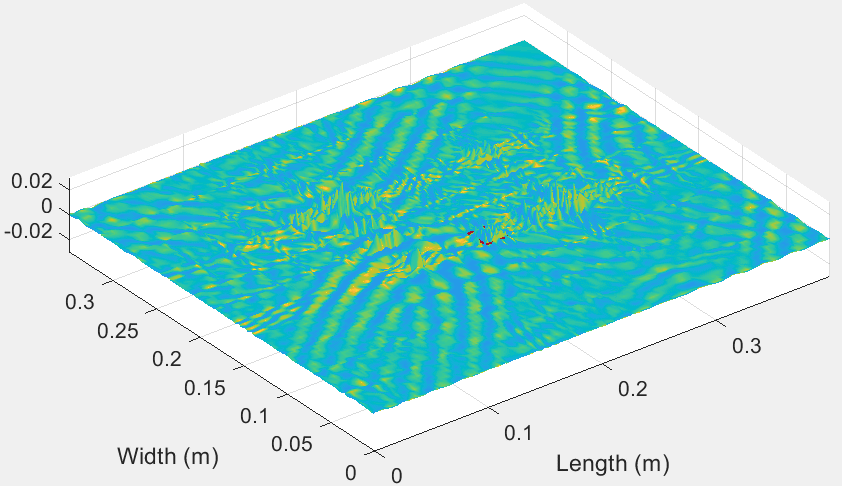
Our laboratory has spent a lot of effort for the development of state-of-the-art numerical methods for the efficient simulation of static and dynamic phenomena in composite structures. The Finite Wavelet Domain (FWD) method has been constructed and pioneering wavelet-based elements using Daubechies scaling functions as basis functions have been created. Moreover, the Time Domain Spectral Finite Element (TDSFE) method has been formed and efficient multi-nodal spectral elements have been employed.
Development of numerical tools for simulation of SMA behavior
- Development of material subroutines implementing SMA constitutive models in 1D and 3D form. The developed subroutines are incorporated into well-established FE Codes, exploiting parallel solvers and advanced analysis techniques.
- Development of specialty beam element for the prediction of complex thermomechanical behavior of SMA actuators. The beam element predicts coupling phenomena, temperature and stress distribution on the cross-section as well as the time response of SMA actuators.
FE for Damped Composite Shell Structures
An 8-node specialty damped shear shell finite element was developed for predicting the damping of laminated composite structures of arbitrary laminations and shapes. The FE encompasses a series of mechanics models enabling integrated modeling of damping from ply to structural level. Evaluations of the developed FE with results from other FEs, analytical solutions and conducted experiments have demonstrated its excellent performance, accuracy and unique predictive capabilities.
Developement of Molecular Mechanics FEs for Graphene
Non-Linear FEs based on uncoupled Molecular Mechanics Potetinal Equations have been developed. The employed parameter set has been optimized for graphene using DFT calculations. The developed models have been incorporated into Abaqus®.
The employed parameter set has been optimized for graphene using DFT calculations. The developed models have been incorporated into Abaqus®.
